Matlab simulation of optical filtering experiment
-
摘要:
光学滤波实验是物理光学课程重要的实验之一,实验通过傅里叶透镜对物体的空间分布函数进行傅里叶变换,获得物体的频谱,再通过一系列光学器件对频谱进行滤波操作。利用相机获得实验中物体的数字图像,通过Matlab软件编程实现该图像的傅里叶变换,获得图像频谱,采用理想高通(低通)滤波器对频谱进行滤波处理,获得滤波后的图像,并将仿真结果与实验结果进行对比。此实验仿真可以使学生深入理解数字图像处理技术中的傅里叶变换和滤波操作的相关内容,使抽象的理论更加形象化、直观化。
Abstract:The optical filtering experiment is one of the important experiments in the physical optics course. In this experiment, a Fourier lens is used to perform the Fourier transform on the spatial distribution function of an object to obtain its spectrum, which is then filtered through a series of optical elements. A digital image of the object in the experiment is captured using a camera, and the Fourier transform of this image is achieved through Matlab software programming, yielding the image spectrum. An ideal high-pass (low-pass) filter is then applied to the spectrum for filtering, resulting in a filtered image. The simulation results are compared with the experimental outcomes. This experimental simulation allows students to deeply understand the concepts related to Fourier transform and filtering operations in digital image processing technology, making the abstract theories more tangible and intuitive.
-
Keywords:
- optical filtering /
- Matlab software /
- digital image processing /
- Fourier transform
-
在数字图像处理技术中,傅里叶变换是一种重要的数学工具。它能够将图像从空间域转换到频率域,对频率域的频谱进行分析和处理,然后再通过傅里叶逆变换得到处理后的图像。这一过程大大简化了复杂问题的处理,特别是在图像增强和图像复原技术中。在这些技术中,常常采用傅里叶变换来获取图像的频谱,并应用滤波模板对频谱进行各种滤波操作,以实现图像的增强或复原[1-2]。然而,对于学生来说,从理论上理解数字图像与其频谱之间的对应关系较为困难。相比之下,物理光学实验中的光学滤波实验提供了一个直观的视角,展示了光学图像本身及其频谱的获取过程。该实验同样以傅里叶变换为理论基础,利用傅里叶透镜实现物体空间分布函数的傅里叶变换,从而获取物像的频谱,并通过使用不同形状的光学滤波片来实现各种滤波操作。
本文巧妙地将光学滤波实验现象与数字图像处理中的频谱分析流程相结合,并利用Matlab软件对光学滤波实验进行了仿真模拟。在实验中,通过相机将实物光学成像转换为数字图像并输入计算机进行傅里叶变换,随后对获得的频谱进行低通滤波处理,并与光学滤波实验现象进行对比分析。结果表明,仿真结果与实验现象能够很好地吻合。通过这一仿真操作,不仅实现了不同课程之间的关联,还有助于学生加深对频谱分析相关概念和原理的理解。同时,这也使得教学内容更加丰富多样,提高了教学质量。
1. 傅里叶变换原理
傅里叶变换是一种重要的数学工具,广泛应用于物理、工程、计算机科学等领域。傅里叶变换是傅里叶级数的推广形式,能够将非周期函数分解为一系列正弦函数和余弦函数的线性组合。傅里叶变换的物理意义在于能够将信号从时域(或空间域)转换到频域,从而更好地分析信号的特征和性质。通过对频域信息进行处理,并利用逆变换,可以重新获得目标信号[3]。以二维傅里叶变换为例[4],变换公式如下:
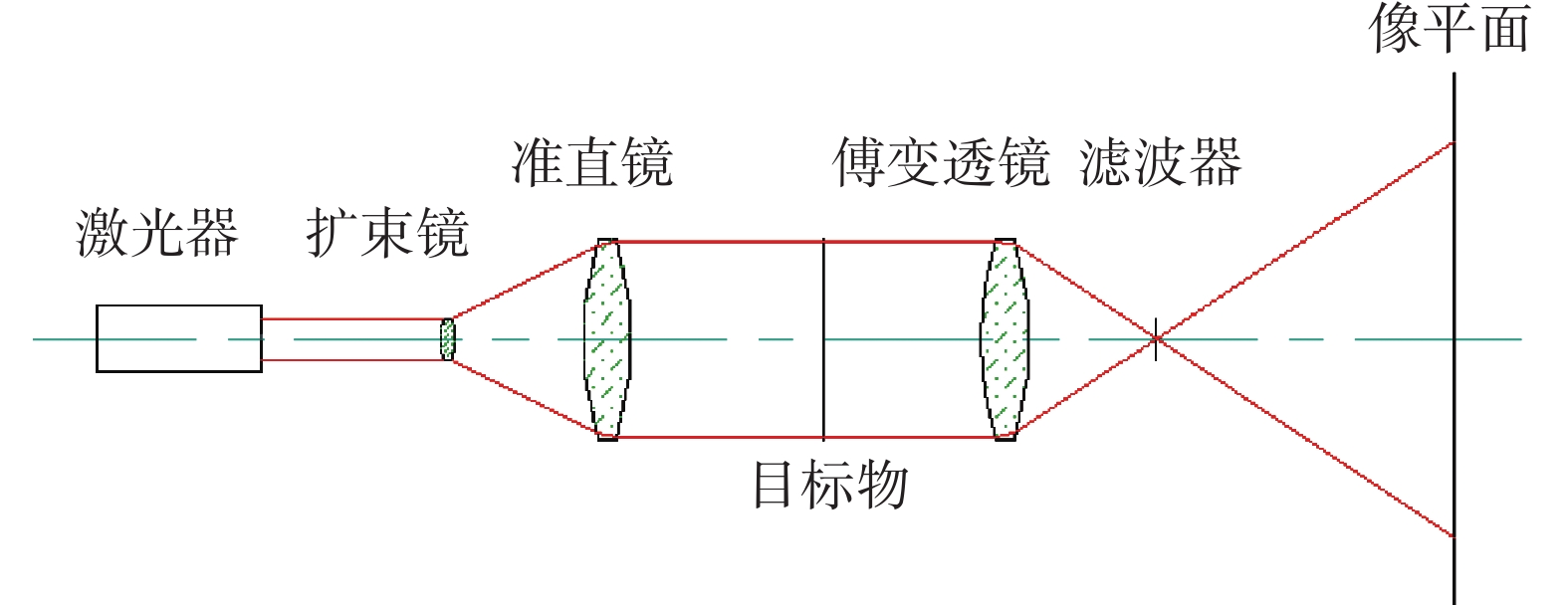
$$ F(u,v)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\mathrm{e}^{-\mathrm{j}2{{\text{π}}}(ux+uy)}\mathrm{d}x\mathrm{d}y $$ (1) 式中:u,v是频率变量;
$ f(x, y) $ 为非周期函数,是该$ {{F}}(u, v) $ 函数在频域上的表示。傅里叶逆变换公式为:
$$ f(x, y)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} {F}(u, v) \mathrm{e}^{{\mathrm{j}} 2 {\text{π}}(u x+u y)} {\mathrm{d}} u {\mathrm{d}} v $$ (2) 傅里叶变换是信号处理中非常重要的技术手段,它可以把一个非周期性的信号转换成一系列简单的、具有不同频率的周期性信号的叠加。通过分析处理这些简单的、周期性信号,可以从另一角度分析问题、解决问题,并使问题变得简单化。在实验分析中,例如在光学滤波实验中,通常使用连续傅里叶变换;但在实际应用中,如数字图像处理技术,则广泛使用离散傅里叶变换[5]。
2. 光学滤波实验原理
在物理实验中,可以利用傅里叶透镜实现物平面分布函数f(x,y)向空间频谱函数
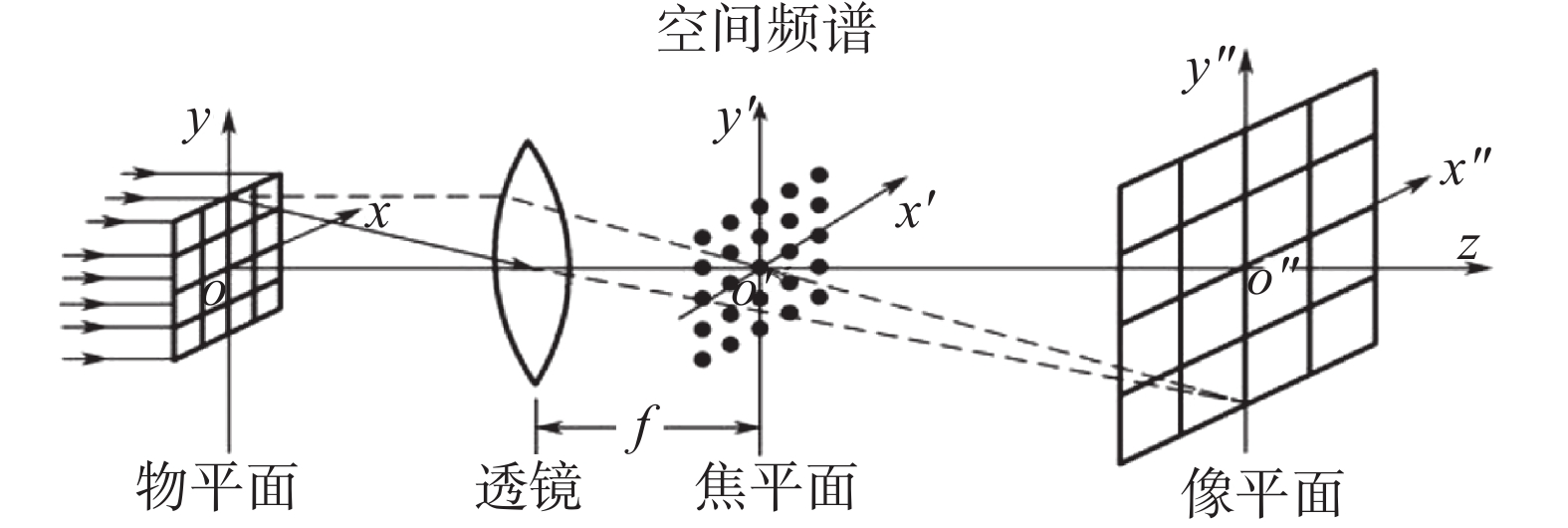
$ F(u, v) $ 的变换。傅里叶透镜是获得物体空间分布函数相应频谱的关键光学器件[6]。相较于普通透镜,傅里叶透镜具有显著优势:普通透镜仅在近光轴区域能正确进行傅里叶变换,而傅里叶透镜则能在整个孔径和视场范围内精确完成这一变换[7],因此,傅里叶透镜不仅要对物成像,还需要对衍射光成像。傅里叶透镜具有2个共轭面:物平面的共轭面得到物体的像;光源所在面的共轭面得到傅里叶变换频谱,其原理如图1所示。图1中靠近中心轴的区域为低频区域,远离中心轴的区域为高频区域。光学滤波实验可以观察到物体频谱获取的详细过程,实验原理如图2所示。实验中选用空间频率为12 L/mm的正交“光”字栅作为物,在傅里叶变换透镜的焦平面上利用光屏观察该正交光栅的频谱点,所选用的“光”字栅的图像和获得的频谱如图3所示。在图2傅里叶透镜的右侧放入低通滤波器后,获得的频谱和相应的“光”字像如图4所示。所用的低通滤波片是中心为小孔的金属片,如图4(a)所示,此滤波片可以滤掉远离光轴的部分高频信息,获得的频谱只留下靠近光轴中心的低频谱图,如图4(b)所示;由于丢失了包含图像细节和轮廓的高频信息,观察到的“光”字像已看不到横竖条纹且边缘变的模糊,如图4(c)所示。若在傅里叶透镜右侧放入高通滤波器,获得的频谱和相应的“光”字像如图5所示。图5(a)为高通滤波片,可以滤掉靠近光轴的部分低频信息,获得的频谱见图5(b),由于丢失了包含大部分能量的低频信息,观察到“光”字像明显变暗,且有部分边缘不可以成像,导致成像不完整,如图5(c)所示。
3. Matlab软件仿真实现傅里叶变换及滤波
在数字图像处理技术中,傅里叶变换是数字图像分析处理的重要手段。通常通过傅里叶变换获得图像的频谱,并对频谱进行分析与处理,进而实现对图像的分析与处理[8-9]。基于此,深刻理解傅里叶变换的原理是对其进行改进、变形应用的基础[10]。本文将光学滤波实验中“光”字栅所形成的光学图像利用数码相机拍照,获得数字图像,并应用Matlab软件进行傅里叶变换。“光”字图像和Matlab傅里叶频谱如图6所示。将获得的频谱与光学滤波实验结果(见图3(b))进行比较分析,进一步理解Matlab傅里叶频谱的物理意义,同时把数字图像处理中比较抽象的傅里叶变换,以更加形象、直观的方式呈现给学生。
获得频谱的Matlab程序如下:
>> I=imread('light1.jpg');
>> J=rgb2gray(I);
>> K=fft2(J);
>> H=fftshift(K);
>> M=abs(H/256);
>> imshow(uint8(M));
实验中使用的低通(高通)滤波器与图像处理技术中的理想低通(高通)滤波器具有相同的原理,理想低通(高通)滤波器传递函数分别为:
$$ H(u,v) = \left\{ \begin{array}{*{20}{l}} 1, &{D(u,v) \leqslant {D_0}} \\ 0, &{D(u,v) \gt {D_0}} \end{array} \right. $$ (3) $$ H(u, v)=\left\{\begin{array}{lc}0, & D(u, v) \leq D_0 \\ 1, & D(u, v)>D_0\end{array}\right. $$ (4) 式中,
$ D(u,v) = \sqrt {{u^2} + {v^2}} $ ,改变阈值D0的大小可以实现不同滤波效果。因此,在Matlab操作中,选用理想低通(高通)滤波器对图6中的“光”字图像的傅里叶频谱进行滤波处理。以理想低通滤波器为例,其Matlab程序如下:>> I=imread('light1.jpg');
>> I=rgb2gray(I);
>> J=im2double(I);
>> M=2*size(I,1);
>> N=2*size(I,2);
>> u=-M/2:M/2-1;
>> v=-N/2:N/2-1;
>> [U,V]=meshgrid(u,v);
>> D=sqrt(U.^2+V.^2);
>> D0=35;
>> H=double(D<=D0);
>> J=fftshift(fft2(I,size(H,1),size(H,2)));
>> K=J.*H;
>>L=ifft2(ifftshift(K));
>>L=L(1:size(I,1),1:size(I,2));
>>subplot(121),imshow(I);
>>subplot(122),imshow(L/256);
由图7可见,经过理想低通滤波器处理之后,原图像中的横竖条纹已经看不清楚,图像轮廓变得模糊,这是因为理想低通滤波器滤掉了反应图像边界或轮廓以及其他像素值变化比较大的部分高频信息,改变了阈值D0的大小,可以调节通过的低频信息范围。此结果和光学滤波实验的结果完全一致。
4. 结 语
本文将具有共同理论基础的光学滤波实验与数字图像处理技术中的傅里叶变换相结合,应用Matlab软件实现了光学滤波实验的仿真操作。在光学滤波实验中形象、直观地展现了“光”字栅图像经过傅里叶透镜进行傅里叶变换的过程,并在光屏上获得了该图像的傅里叶频谱。这一过程实现了图像从空间域到频率域的相互转化,使学生能够更加深刻地理解图像和频谱之间的变换关系。在实验中,还应用了低通(高通)滤波片对频谱进行滤波,分析低(高)频信息与图像信息之间的对应关系。同时,应用Matlab软件将“光”字的数字图像进行了傅里叶变换,获得其傅里叶频谱。随后,利用理想低通滤波器对频谱进行滤波操作,获得了与光学滤波实验现象相吻合的数字图像。换言之,本文将以计算机为载体的数字图像处理技术中的傅里叶变换及滤波处理,通过物理光学实验的形式展现,有效地实现了相关知识的融合理解。
-
-
[1] 谢勇,贾惠珍,王同罕,等. 图像去雾算法综述[J]. 计算机与数字工程,2022,50(12):2765-2774. DOI: 10.3969/j.issn.1672-9722.2022.12.031 [2] 张勇. 傅里叶变换在数字图像处理中的应用[J]. 廊坊师范学院学报(自然科学版),2015,15(3):25-27. DOI: 10.3969/j.issn.1674-3229.2015.03.007 [3] 任鸿鹏. 基于傅里叶变换的Matlab图像处理[J]. 科技资讯,2019,17(16):11-12. [4] 杨杰,黄朝兵. 数字图像处理及Matlab实现[M]. 3版. 北京:电子工业出版社,2019. [5] 翟中生,段浪,郑雅雯. 基于SLM的几何稳相法光束整形影响因素分析[J]. 应用光学,2023,44(4):711-719. [6] 王彦杰. 离散傅里叶变换在实际中的应用[J]. 宁德师范学院学报(自然科学版),2019,31(4):337-343. [7] 安葆青,相里斌,高瞻,等. 全对称傅里叶透镜的设计[J]. 光子学报,1997,26(10):956-959. [8] ZHANG Z H,GUO H W. Fringe phase extraction using windowed Fourier transform guided by principal component analysis[J]. Applied Optics,2013,52(27):6804-6812. DOI: 10.1364/AO.52.006804
[9] GÓMEZ-ECHAVARRÍA A,UGARTE J P,TOBÓN C. The fractional Fourier transform as a biomedical signal and image processing tool:a review[J]. Biocybernetics and Biomedical Engineering,2020,40(3):1081-1093. DOI: 10.1016/j.bbe.2020.05.004
[10] YU S S,ZHOU N R,GONG L H,et al. Optical image encryption algorithm based on phase-truncated short-time fractional Fourier transform and hyper-chaotic system[J]. Optics and Lasers in Engineering,2020,124:105816. DOI: 10.1016/j.optlaseng.2019.105816



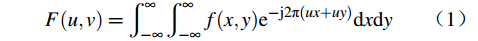
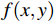
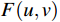
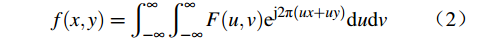
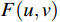
 下载:
下载:




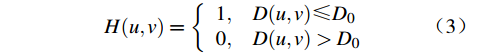
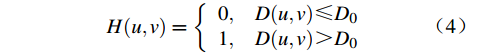
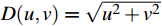
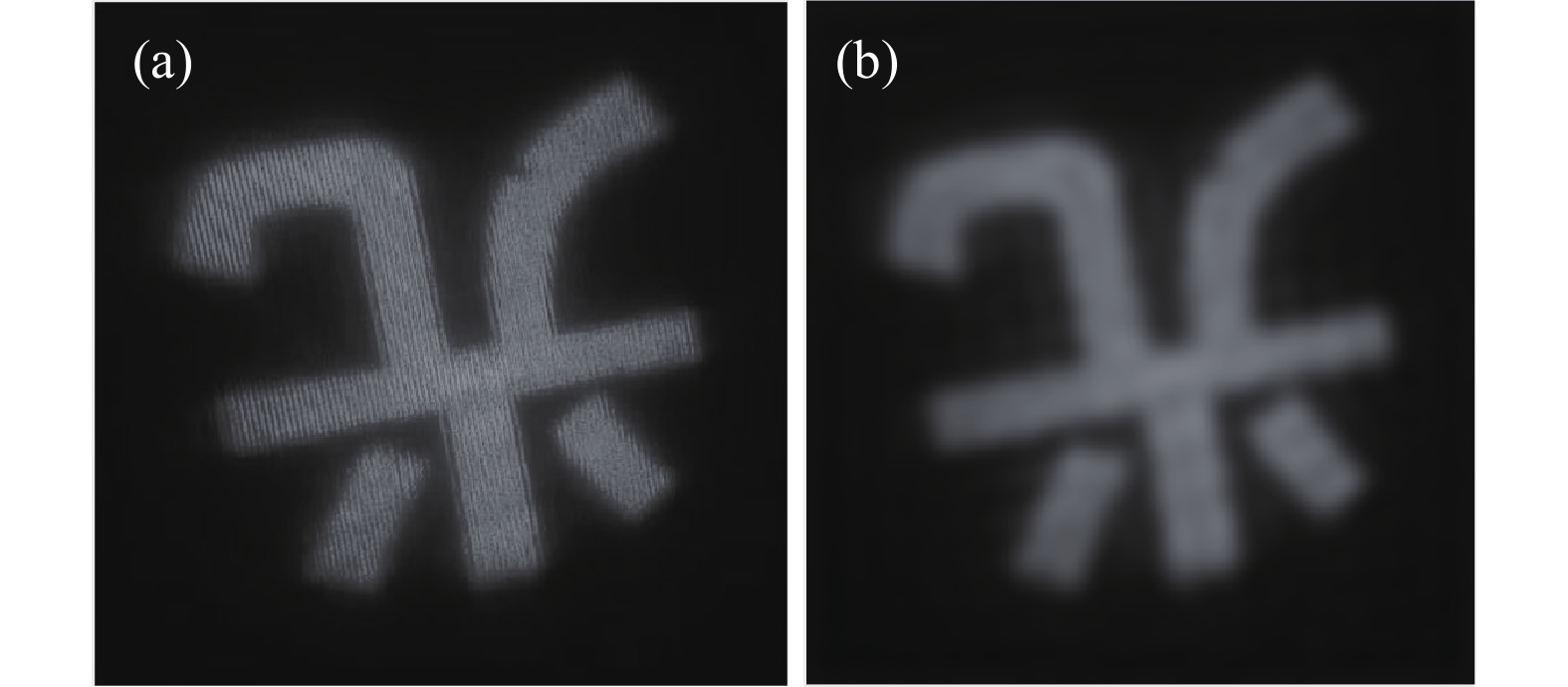



 地址:上海市漕宝路120号
地址:上海市漕宝路120号 电话:021-64691562
电话:021-64691562  邮箱:
邮箱: 版权所有:《应用技术学报》编辑部
版权所有:《应用技术学报》编辑部